Excellent job shop scheduling does not require fancy tools

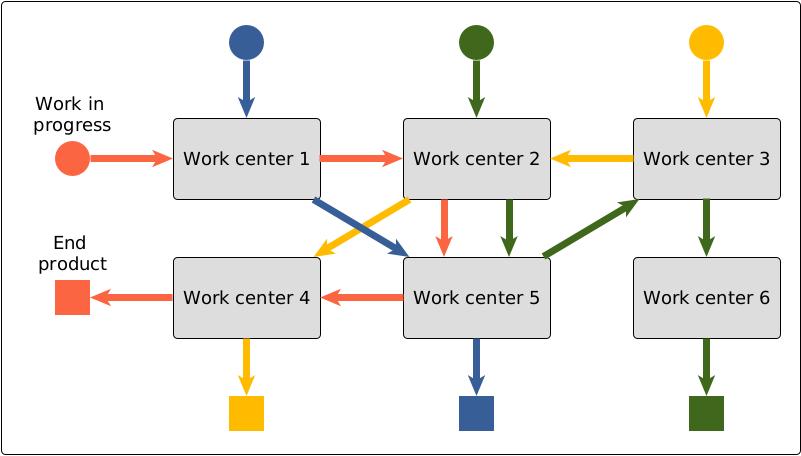
This post is about job shop scheduling (production scheduling in job shops). Job shops are factories that process jobs that require processing at multiple workstations, where the subset and order of workstations vary between jobs. The principle is illustrated in the figure below. Examples are the manufacturing of customized products like computer servers to customer order, or hospitals where each patient is considered a job needing a unique sequence of treatments. The overall production process is relatively complex because of the special requirements per type of job. Moreover, demand fluctuates and is hard to predict, and bottlenecks and underutilization frequently occur at different work centers. Workstation utilization can be improved by making sure that there are always enough jobs waiting. However, that increases cycle times and work in progress (WIP) and complicates short-term reprioritization. Without a form of decision support, finding a good production schedule is a challenging task.

Optimization with Python in Excel

Many companies use Excel for their job shop scheduling as a flexible and familiar tool without additional costs. It is however difficult to create efficient schedules while considering equipment, personnel and material constraints. Macros (VBA) increase Excel’s capabilities, but it’s a cumbersome programming language with many oddities and it executes slow, which becomes a problem when operating with large amounts of data. There are alternatives to Excel, but they are not as lightweight (see here). A compromise is to use an Excel–plugin called SolverStudio, which allows you to build and solve optimization models in Excel. Optimization models are written in Python and can be solved with different solvers such as the free Cbc from COIN-OR, Gurobi, or CPLEX. Such a solution can serve as a proof of concept to explore the potential and limits of an optimization approach, but planners often stick with such a solution.

A basic job shop scheduling model

The job shop problem can be outlined as follows: There is a set of machines and a set of jobs. Each job consists of a series of operations that must be executed one after the other. Each operation needs processing on a specific machine. Processing takes a given duration, and once it has started, it cannot be interrupted. A machine can only execute a single operation at a time. Common objectives are to minimize delays with respect to order due dates or minimize costs or minimize the makespan, which is the total time until all jobs are completed. A solution (i.e., a schedule) specifies the start time of each operation. You can download an exemplary spreadsheet here, enter your data, and run optimizations. The README on the first sheet explains how to use the spreadsheet. In this example, the objective is to minimize the makespan.

More realistic situations

In practice, we need to consider many additional issues. Examples are …

• Sequence-dependent setup times, e.g., in a paint shop we can switch from bright to dark colors without cleaning, but cleaning is required when switching from a dark to a bright color.
• Work station availability constraints, e.g., work stations are unavailable at times due to holidays, maintenance, etc.
• Complex dependencies between operations, e.g.,
  • the successor can start once its predecessor is completed 50%,
  • the successor must start exactly when its predecessor completes (no–wait), or
  • a machine is not allowed to be idle between executions (no–idle).
• Parallel machines: it is possible to select one of multiple machines for an operation.
• Trade off between different objectives, e.g., reduce cycle time and WIP.
• Resources: assign limited shared resources such as special tools.

Conclusion

Mathematical optimization has the potential to significantly improve production schedules. However, the complications mentioned can sometimes lead to very difficult or even impossible-to-solve optimization models. Sometimes we have to explore to find out, and SolverStudio offers a lightweight way to do that without leaving Excel. This spreadsheet-based solution can be a stepping stone toward more sophisticated solutions, or a long–term solution if issues like integration with the manufacturing execution system are not too important.